Частотная характеристика линейной непрерывной стационарной системы (ЛНС)

            Ранее (лекция 3) было показано, что выходной сигнал ЛНС во временной области  представляет собой свертку входного сигнала и импульсной характеристики системы

Получим  преобразование Фурье свертки

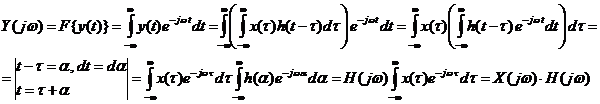
Следовательно,  выходной сигнал в частотной области

 ,

где    - преобразование Фурье  (спектр) входного сигнала,

           - частотная характеристика или комплексный коэффициент передачи системы (ЧХ, англ. frequency response).  

Выходной сигнал во временной области может быть найден через  обратное преобразование Фурье от  Y(jω)      .

Модуль частотной характеристики   - называется амплитудно- частотной характеристикой  (АЧХ - amplitude response) системы, аргумент   - фазочастотная характеристика (ФЧХ – phase response).

Частотная характеристика системы  является  преобразованием Фурье её импульсной характеристики, т.е. .  Она  может рассматриваться  также как реакция (отклик) системы на входное воздействие в виде комплексной гармоники   e^jωt. 

Действительно,

,

т.е.   . Поскольку  , то на практике (экспериментально) АЧХ реальной системы определяется подачей на её вход действительной гармоники и измерением отношения амплитуды выходной гармоники к амплитуде входной гармоники. ФЧХ – это разность фаз выходной и входной гармоник определенной частоты.  Обе характеристики – функции частоты f  или ω. Соответствующие приборы называются измерителями частотных характеристик.

Выражение                                  

является основным выражением анализа ЛНС в частотной области. Оно означает, что комплексный спектр (преобразование Фурье) выходного сигнала равен произведению спектра входного сигнала на частотную характеристику системы.

Поскольку это просто умножение, то анализ в частотной области значительно проще и удобнее, чем вычисление интеграла  свертки во временной области. Во многих приложениях  частотный метод  является основным методом анализа линейных систем.

Далее в курсе частотная характеристика будет рассматриваться более подробно.

Свойства  преобразования Фурье

            В практических задачах обработки сигналов широко используются свойства, которыми обладает преобразование Фурье (НВПФ).

1.    Свойство линейности (linearity)

   или 

Доказательство:

2.  Свойство симметрии (symmetry) преобразования Фурье  .

            Произвольную действительную (некомплексную) функцию x(t) можно представить суммой четной (even) и нечетной (odd) составляющих, т.е.    ,

где  - четная функция аргумента,

        - нечетная  функция аргумента.

С учетом этого представления спектральная плотность сигнала

.

Здесь   -  вещественная часть X(f),  косинус-преобразование Фурье, четная функция частоты   f,

 - мнимая часть X(f), синус-преобразование Фурье, нечетная функция частоты   f.   

Отсюда амплитудный спектр  - четная функция  частоты,

фазовый спектр   - нечетная функция частоты.

Поэтому достаточно рассматривать и вычислять спектры для положительных частот.

 

3. Свойство дуальности (duality)

 Математически прямое и обратное преобразования Фурье различаются только знаком показателей экспонент,  .    Возьмем второе выражение (ОПФ), заменим  f→b, .  Отсюда при замене  t→-f получаем     -  прямое преобразование Фурье.  Итак, если   функции x(t)  в частотной области  соответствует X(f), т.е. , то  функции X(t) во временной области отвечает преобразование Фурье вида x(-f), т.е. .

Это означает, что если мы знаем  одно выражение  из известной пары преобразований Фурье, то по нему  мы можем  определить  другое.      Графическое пояснение:

Прямоугольный импульс как функция времени имеет спектральную плотность (спектр) вида    sin x/x  (см. пример из лекции 6).   Отсюда сигнал вида   sin t/t   во  временной области  имеет спектр в виде прямоугольного импульса  в частотной области.

Другой пример:     (см. лекцию 6),  здесь   u(t) - единичный скачок.  Отсюда по свойству дуальности    комплексный  сигнал       должен иметь спектр вида , т.е. .

 

4.      Свойство временного сдвига (shift in t)

При сдвиге сигнала во времени на t₀ модуль преобразования Фурье  (амплитудный спектр) не изменяется, добавляется только фазовый сдвиг (-2πft₀), т.е.

.

Доказательство:  по определению  преобразования Фурье

.

Таким образом, при сдвиге сигнала во времени его амплитудный спектр не изменяется, только линейно сдвигается  фазовый спектр (фаза) на  величину –j2πft₀.

5.  Свойство модуляции или  частотного сдвига (shift in f)
            Сдвиг аргумента спектральной плотности  X(f) по частоте на  f₀  эквивалентен умножению во временной области на множитель

.

Доказательство: .

Умножение комплексной экспоненты с частотой f₀ на функцию x(t) математически означает  амплитудную модуляцию (АМ) комплексной экспоненты (комплексной несущей) низкочастотным сигналом x(t).    Разновидности  АМ с гармонической несущей

 - сигнал с косинусоидальной несущей,

 - сигнал с синусоидальной несущей.

.

В  АМ радиовещании (длинные и средние волны)  амплитудно – модулированный сигнал имеет вид  , где константа m – это  индекс модуляции.

В соответствии со свойством модуляции     , т.е. при модуляции спектр X(f)  сигнала x(t) сдвигается в частотной области на частоту несущей.

Представив по формуле Эйлера  , получим   , т.е. при модуляции косинусоидальной несущей спектр исходного сигнала x(t) сдвигается в частотной области влево и вправо на   f₀.  

Т.о., при АМ происходит перенос низкочастотного спектра сигнала на частоту модуляции f_0. Более подробно модуляция сигналов будет рассматриваться в лекции 17  курса.

6.   Свойство дифференцирования по времени (differentiate in t)
                                    .

Доказательство: если , то

Обобщая полученный результат, получаем    .  

Следствие.  Соответствие между обыкновенным линейным дифференциальным уравнением  N – го порядка во временной области  и его видом в частотной области

Каждому слагаемому вида  соответствует  в частотной области.

Дифференциальное уравнение во временной области соответствует алгебраическому относительно частоты уравнению в частотной области.

7. Свойство временного  масштабирования  (time scaling)

                                         .

Доказательство:    .

В частности, для  a = -1  (реверсирование во времени) получаем       .

 На  рис. приведены графики  прямоугольных импульсов и их амплитудных спектров для  длительностей  τ₁ = 10 с  и  τ₂=1 с.

Как видно из графиков, более узкий импульс имеет более широкий спектр.

Наоборот, если сигнал расширяется  (a < 1) , то спектр сужается с сохранением площади.

Это  следует из свойства временного масштабирования.

8.  Свойство моментов нулевого порядка (zeroth-order moments)
Из определения преобразования Фурье    следует                           и    .

 

X(0) и  x(0) называют  моментами нулевого порядка сигнала в частотной и временной области.  При этом - постоянная составляющая сигнала x(t), т.е.  значение X(f)  на частоте f =0,   x(0) – значение x(t) в начале координат (t=0).

Например, для прямоугольного импульса длительностью   τ = 2Т₁ = 1 с и X(0) =1

Спектральная плотность    .  Отсюда

9. Свойство свертки (convolution)

Пусть  - свертка (convolution) функций   x₁(t) и x₂(t).
 Тогда преобразование Фурье свертки

Таким образом, свертке двух функций во временной области соответствует произведение их преобразований Фурье в частотной области

.

Это свойство является важнейшим в частотном анализе линейных    динамических систем,

(см. начало лекции)

 

 

           

 

 

На основании дуальности преобразования Фурье можно также утверждать, что произведению функций во временной области соответствует свертка в частотной области,

,

здесь * - символ свертки, но это свертка X₁ (f)  и X₂ (f) в частотной области.

 

Соответствие между длительностью сигнала и шириной его спектра

            Согласно свойству временного масштабирования преобразования Фурье

Следовательно,  расширение сигнала во времени (a<1) при сохранении его формы приводит к сжатию спектра сигнала и наоборот, сужение сигнала (a>1) сопровождается расширением  его спектра.  Поэтому для любого действительного сигнала справедливо соотношение

,

где  - длительность сигнала,

       = В - ширина спектра или полоса частот сигнала  (Band), т.е. интервал частот, в котором    заключена основная часть энергии сигнала,

        - константа, значение которой зависит от формы сигнала, для большинства реальных сигналов принимается  .

Это соотношение называется принципом неопределенности в теории сигналов. Согласно этому принципу, чем меньше длительность сигнала  , тем шире его полоса частот  .

   Это, в частности  означает, что прямоугольный импульс длительностью 1 с  имеет полосу частот  порядка 1 Гц, длительностью 1 мс -  1 кГц, длительностью 1 мкс -  1 МГц и т.д.

      Соотношение неопределенности часто используется на практике для приближенной оценки полосы частот сигнала. Например, для телефонной связи  полоса частот  речевого сигнала 300-4000 Гц,  для ЭКГ – сигналов  0-100 Гц (уже!), для аудиосигналов полоса частот  20 Гц – 20 кГц  (шире!).

 

Одно из следствий  обсуждаемого результата. В каналах передачи двоичных цифровых данных, т.е. последовательностей 1 и 0,  один импульс соответствует одному биту информации. Чем больше импульсов передается за секунду, тем меньше длительность одного бита, тем больше скорость передачи в бит/с.  Следовательно, тем более широкая полоса частот необходима для передачи информации. Отсюда терминология: широкополосный канал, широкополосный  Internet и т.п.

Формула Шеннона для максимальной пропускной способности (скорости передачи информации в бит/с)  канала передачи информации имеет вид

                                               .

Здесь   P_C – мощность сигнала,   P_ш – мощность шума в канале,  - отношение сигнал-шум  (отношение мощности сигнала к мощности шума).    Таким образом, пропускная способность канала  C (бит/с) пропорциональна  его полосе частот F.  Чем шире полоса частот канала, тем выше скорость передачи информации (бит/с) по данному каналу.

В  теории сигналов  применяется понятие  база сигнала - это произведение эффективного значения длительности сигнала  и эффективного значения ширины его спектра  .  Длительность сигнала и ширина его спектра подчиняются неравенству неопределенности, гласящему, что база сигнала не может быть меньше единицы. Но ограничений на максимальное значение базы сигнала не существует. То есть короткий сигнал с узким спектром существовать не может, а сигнал большой длительности (теоретически - бесконечной)  с широким спектром — может (так называемый широкополосный сигнал, сигнал с большой базой). В настоящее время такие сигналы широко применяются в технике связи.

Их называют также шумоподобными сигналами.

Преобразование Фурье периодического сигнала

            Преобразование Фурье для периодического сигнала не существует, поскольку энергия его бесконечна.  Но с  помощью дельта - функции можно выразить преобразование Фурье и для периодического сигнала. Хотя такой подход   - искусственный с позиций математического анализа.    Но в обработке сигналов он используется и распространен. Рассмотрим его сущность.

Предположим, что  . Тогда обратное преобразование Фурье  дает нам     ( по свойству фильтрации дельта – функции). 

Следовательно, преобразование Фурье  комплексной гармоники имеет вид

 - свойство модуляции.

Поскольку преобразование Фурье являются линейным преобразованием (свойство линейности),  то можно записать более общее выражение

.

Здесь  x(t)  - ряд Фурье , X_k – коэффициент ряда Фурье периодического сигнала.

Таким образом, преобразование Фурье (спектр) периодического сигнала может быть представлено через дельта – функции  как взвешенная сумма периодической последовательности  дельта – функций  (дельта - импульсов) с частотами . Весами являются коэффициенты ряда Фурье периодического сигнала.

 Как следствие, преобразование Фурье (спектр) косинусоидального сигнала (гармоники)

    имеет вид     

,    т.е.  представляется  двумя δ – импульсами с интенсивностью π (множителем) на частотах  ± ω₀ .  

Заключение

§  Выходной сигнал линейной системы  в частотной области

 ,  где    - преобразование Фурье (спектр) входного сигнала,   - частотная характеристика системы.    Во временной области связь выхода и входа имеет вид интеграла свертки

• Преобразование Фурье (НВПФ) имеет ряд важных характерных свойств:
  - симметрии,
  - линейности,
  -  временного сдвига,
  -  частотного сдвига,
  -  дифференцирования,
  -  временного масштабирования,

-  свертки.
Эти свойства широко используются в практических задачах.

§  Соотношение (неравенство)  неопределенности теории сигналов
устанавливает, что чем меньше длительность сигнала  , тем шире его полоса частот (ширина спектра)  и наоборот. Это соотношение часто  применяется на практике.