Некоторые специальные сигналы

Такие сигналы (функции) широко используются в задачах обработки сигналов.

1.                  Гармонические сигналы (гармоники)
   а)  Косинусоидальная гармоника непрерывного времени  (НВ)

Это обычная  тригонометрическая  функция косинуса

 

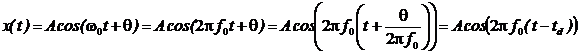
Параметры:  амплитуда А,  частота  [ Гц],   период ,  угловая  частота, ,  θ [рад] – начальная фаза в радианах,    - временной сдвиг (задержка)  в секундах.

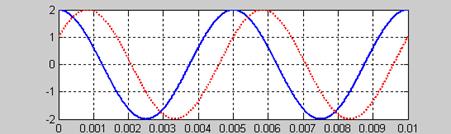
В  данном примере   A = 2,  f₀ = 200 Гц,     с.

В дальнейшем будет показано, что любой периодический сигнал  x(t)  с периодом   можно представить в виде бесконечной суммы гармоник  (рядом Фурье)

.

Такое  представление очень важно и продуктивно для многих прикладных наук, в том числе для обработки сигналов.

 

Геометрическая интерпретация гармонического сигнала.

Вектор А вращается против часовой стрелки с частотой  f  или скоростью  радиан/с.

Проекция вектора  А на горизонтальную ось – это значения косинусоидальной гармоники с амплитудой А, на вертикальную ось - значения синусоидальной  гармоники.  Частота     f = 2 Гц означает, что точка делает 2 оборота в сек.

 Если вектор делает один оборот за Т секунд, то угловая скорость (частота)  составляет рад/с.  Θ – начальная фаза (начальный угол) вектора  относительно оси абсцисс.

По формуле  Эйлера   .   Отсюда

Действительная гармоника может быть представлена также  как сумма проекций  двух комплексных гармоник. Одна – проекция вектора половинной амплитуды, вращающегося против  часовой стрелке со скоростью ω рад/с , вторая – такая же проекция вектора, вращающегося по часовой стрелке со скоростью    - ω рад/с.  Первая проекция называется синфазной составляющей, вторая – квадратурной.

 

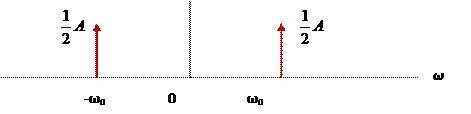
Представление действительной гармоники в  виде суммы комплексных гармоник .  Её график в частотной области

 

б)  Гармоника дискретного времени (ДВ) 

, n-номер отсчета.  Пример:

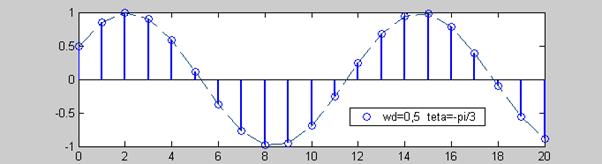
Такая гармоника получается дискретизацией (взятием отсчетов, англ. sampling) из  аналоговой гармоники с  интервалом  (периодом) отсчетов  Т_S=1/F_S или частотой отсчетов   F_S :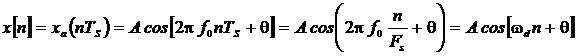 

При этом   f _d  =f₀ /F_S – нормированная  частота в Гц на отсчет ,    - скорость, или частота отсчетов,  - угловая нормированная  частота в радианах в секунду на отсчет,   .  Её называют также цифровой частотой.

Дискретная гармоника периодична с периодом 2π.  Действительно

.

2.                  Дельта-функция (другое название – единичная импульсная функция или функция Дирака).  Это особого вида функция δ(t), определяемая следующим интегралом    .  Отсюда, полагая   f(t)=1, получаем условие для площади  дельта – функции .   Т.о., площадь дельта – функции равна 1.  Интуитивное определение дельта - функции, как предела прямоугольного импульса единичной  площади

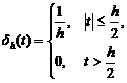.         График   

Определение  дельта-функции:

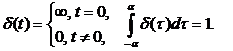
Как следствие,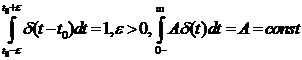   

Условное графическое изображение дельта – функции  

Дельта-функция имеет строгий математический смысл только в том случае, когда она используется под знаком интеграла,   - свойство фильтрации или отсчета функции   f(t), например,   .

 

3.                                          Единичный импульс.  Играет ту же роль для  дискретных систем, что и

что и δ – функция для непрерывных систем.  

                    Соответственно   

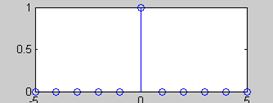
С помощью единичного импульса произвольный дискретный сигнал (последовательность …x(0), x(1), x(2), …) может быть записан как  сумма  вида

4.       Единичная ступенчатая функция (сигнал)
 как следствие   

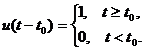
График

                              

 

Функция u(t) имеет разрыв (скачок) при t = 0.

Связь между ступенчатой функцией  u(t) и   дельта – функцией     δ(t)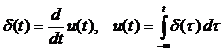   

        

.       Единичная импульсная последовательность

     

 

6.      Аналитические сигналы

            В системах передачи информации (системах связи)  очень часто используются узкополосные сигналы  вида  .  Функция A(t) такого сигнала называется амплитудной огибающей, а  θ(t) – фазовой функцией сигнала.  Математически такие сигналы удобно описывать как комплексные  . При этом  действительный сигнал  x(t) является вещественной частью комплексного сигнала  z(t), т.е. .

            Частным, широко используемым  на практике случаем комплексного сигнала является аналитический сигнал

,

в котором  мнимая часть  вычисляется с помощью преобразования Гильберта (Hilbert transformation)     .

Обратное преобразование Гильберта

определяет  сам сигнал x(t) по его преобразованию  Гильберта . 

Понятие системы.  Линейные системы.

В широком смысле системой называют совокупность элементов, взаимосвязанных между собой таким образом, что возникает определенная целостность, единство. Система обладает свойством иерархичности, в соответствии с которым  каждый компонент (элемент) системы может также  рассматриваться как система, а данная система может являться  элементом более широкой системы.    

В данном курсе рассматриваются линейные системы преобразований сигнала  с одним входом и одним выходом.  При этом физическая природа систем не рассматривается, точнее,  она не имеет главного значения.  Разные физические системы могут описываться одинаковыми уравнениями.

Обозначение   y = L(x) означает  формальное описание преобразования входного сигнала x в выходной y.    Общее графическое обозначение, 

 

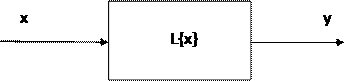
L – это оператор преобразования системы, т.е.  правило (уравнение, функция, алгоритм) преобразования  множества X (входных сигналов) в множество Y  (выходных сигналов).  

 Непрерывные (аналоговые) системы, такие, как устройства аналоговой электроники  или датчик температуры, имеют непрерывный во времени входной x(t) и выходной сигналы y(t).    У дискретных (цифровых)  систем входной  x[n] и выходной сигналы  y[n] – дискретные во времени, как, например, в компьютерах или цифровых процессорах. 

В линейных системах оператор должен обладать свойством  суперпозиции, т.е.

В частности, для линейных систем  нулевой вход влечет нулевой выход

Основным видом оператора системы является уравнение связи выходного и входного сигналов. Для линейных систем уравнение является линейным. Большой класс реальных систем, но не все,  описывается линейными дифференциальными и разностными уравнениями.

Примеры линейных систем.

1. Линейными являются линейные электрические цепи, например,  LRC – цепь (контур)

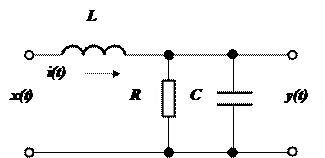
Уравнения цепи. Из законов Киргофа

Если  , и  ,  то

Т.е. сумме входных сигналов соответствует сумма выходных сигналов – линейная система.

2.  Линейная активная электрическая цепь, например,  интегратор

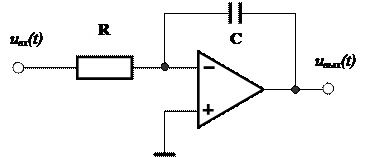
В обозначениях курса ТОС:     

Уравнения системы:  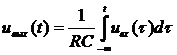         ,  если  , то       ,  т.е. система  является линейной.

3.    Линейные  дискретные системы, описываемые линейными разностными уравнениями.

  Например, дискретный фильтр   текущего усреднения с уравнением , при этом М – число усредняемых  точек. В этом фильтре каждая точка выходного сигнала   определяется как среднее арифметическое предыдущих  М точек входного сигнала,  в результате - уменьшаются шумы  Система – линейная, что легко проверяется.

Для нелинейных систем принцип суперпозиции неприменим. Поэтому анализ нелинейных систем значительно сложнее, чем линейных.

Примеры нелинейных систем:   системы со статическими нелинейными характеристиками, например, транзисторы, диоды, а также  умножители сигналов, электронные устройства типа модуляторов, детекторов, преобразователи формы сигналов и др.

Многие нелинейные системы являются линейными в режиме малого сигнала, например, транзисторные усилители, операционные усилители, что упрощает их анализ.

Нелинейные системы в данном курсе не рассматриваются.

Безынерционные и инерционные системы

                Система является безынерционной  или системой без памяти (memoryless system),  если её выходной сигнал зависит только от настоящих значений входного сигнала, но не зависит от прошлых и будущих значений. В противном случае система является инерционной или системой с памятью (memory system). Например, квадратор с уравнением  - это безынерционная  нелинейная система.  Любая цепь, состоящая только из резисторов – безинерционная, т.к. резистор -  безынерционный элемент.

Другой пример.    RC – цепь (фильтр нижних  частот) с уравнением     - это система (цепь) с памятью (инерционная).

Физически реализуемые (каузальные)  системы

Физически реализуемой, или каузальной (англ. causе - причина ) является система,  выходной сигнал которой в момент времени t₀ зависит только от  прошлых и настоящих значений входного сигнала, но не от будущих.

Пример каузальных систем:  интегратор  или  цепь задержки . Некаузальная система:  . Все системы реального времени – каузальные.  Время изменяется только  вперед. Но системы, обрабатывающие данные, сохраненные в памяти (off – line systems) процессора, могут быть некаузальными.

Некаузальными могут быть  систем с пространственными переменными, обычно обозначаемыми как  x ,y и др.  Пространственная переменная может изменяться в любом направлении.

Стационарные (инвариантные во времени) системы

                Система является стационарной, или инвариантной во времени (англ. time invariance system),  если временной сдвиг сигнала на входе вызывает такой же сдвиг сигнала на выходе системы. Для стационарной  системы  непрерывного времени  справедливо, если , то  .   Стационарные системы – это системы с постоянными во времени параметрами. Во многих практических задачах  обоснованно предполагается стационарность системы, что упрощает их анализ.  В данном курсе рассматриваются только линейные инвариантные во времени системы  (ЛИВ или ЛСС  системы). Англ. LTI systems - линейные инвариантные во времени системы.

Устойчивые  и неустойчивые системы

Если ограниченному входному сигналу  всегда соответствует ограниченный выходной сигнал  , то система является устойчивой. Мнемоника:  ограниченный вход   à  ограниченный выход (ОВОВ).

Для большинства (но не всех!) систем устойчивость является обязательным условием их работоспособности.

Например, система – усилитель

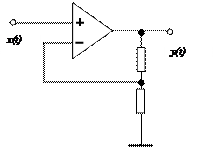
с уравнением 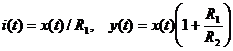  - устойчивая  система, ограниченному входу  соответствует ограниченный выход.    Интегратор с уравнением  )   (см. схему выше)  - неустойчивая система, поскольку, если  , то выходной сигнал неограниченно возрастает с увеличением времени интегрирования  t.

Заключение

·               В анализе и синтезе систем широко используются специальные сигналы, такие как
- дельта функция 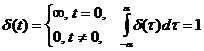 ,   - для систем  НВ,
- единичный импульс 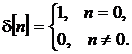  ,  - для систем ДВ,
- единичная ступенчатая функция 

- единичная импульсная последовательность 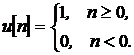 ,   для систем ДВ
- гармонический  сигнал  (гармоника) .

·               Система – это объект (устройство), в котором определены связи между входными и выходными сигналами в соответствии с его структурой и параметрами.
Системы подразделяют на:

- линейные и нелинейные – важнейший признак классификации для обработки сигналов,

- инерционные и безынерционные,

- стационарные и нестационарные,

- каузальные (физически реализуемые)  и некаузальные,

- устойчивые и неустойчивые.