Цифро – аналоговое преобразование сигналов

После дискретизации и  цифровой обработки сигнала  во многих практических задачах  необходимо вновь преобразовать его в аналоговый, например, для воспроизведения звукового сигнала через акустические колонки или для получения изображения на аналоговом мониторе компьютера.

Для преобразования цифровых сигналов в аналоговые используются цифро – аналоговые преобразователи (ЦАП, англ. Digital – to –Analog Converter,  DAC или D/C).  ЦАП является компонентом, в частности, звуковой карты, а также видеоадаптера РС.  Структурная  схема, поясняющая место  ЦАП в обработке сигнала

 

 

 

 

 

На  вход стандартного  ЦАП поступает цифровой сигнал с выхода ЦП в параллельном  коде. Сигнал на выходе ЦАП имеет ступенчатый характер.  Для сглаживания (удаления высокочастотных составляющих)  этого сигнала используют ФНЧ.

Принципы действия и схемы ЦАП рассматриваются в курсах схемотехники. Целью данной лекции является рассмотрение вопросов, связанных с математическим представлением процесса восстановления аналогового сигнала по его отсчетам.

 

 

 

 

 

            Математическая модель восстановления аналогового сигнала по его отсчетам
в частотной  области

Рассмотрим задачу преобразования цифрового сигнала в аналоговый, иначе  – восстановление (recovering) аналогового сигнала по его отсчетам, используя анализ  в частотной области.   Схема, поясняющая   восстановление сигнала:

 

 

Цель -  получить аналоговый (восстановленный) сигнал  по его отсчетам  .

Выражение дискретного  по времени сигнала при идеальной дискретизации:

 - последовательность  смещенных δ – функций, модулированная  отсчетами исходного аналогового сигнала.

Как показано ранее, спектр дискретного сигнала x_p(t)

,    –  угловая частота отсчетов.

 

Полагаем, что сигнал принадлежит к сигналам с ограниченным спектром и  верхняя граничной частотой ω_m < ω_s /2.   Для выделения основной полосы спектра с k = 0 следует пропустить дискретный сигнал x_p(t) через идеальный  ФНЧ c частотной характеристикой (идеальный  ФНЧ)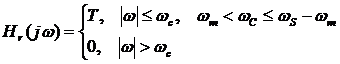 

 

 

 

 

 

 

 

 

 

 

 

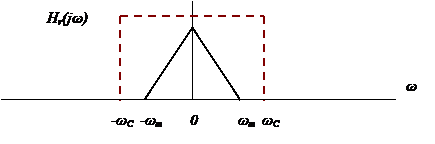
Выходной  сигнал фильтра в частотной области – произведение основной полосы и ЧХ:

               - спектр аналогового сигнала.

Обратное преобразование Фурье  этого спектра   дает исходную (без искажений) функцию сигнала  x(t)  во временной области.  Таким образом, если дискретизация производится с частотой  , то, пропуская дискретный сигнал через идеальный ФНЧ с частотой среза  , можно точно восстановить спектр исходного аналогового сигнала, а, значит, и сам сигнал.  Идеальный ФНЧ практически  не реализуем, его можно воспроизвести только приближенно.  Поэтому на практике восстановить сигнал по его отсчетам  с помощью  реального ФНЧ можно только приближенно.

Математическая модель восстановления аналогового сигнала по его отсчетам
во  временной   области

Выходной  сигнал восстанавливающего фильтра в частотной области

представляет собой произведение спектра (преобразования Фурье) дискретного сигнала и частотной характеристики фильтра.  Произведению преобразований Фурье во временной области соответствует свертка, т.е. выражение выходного сигнала во временной области  - это свертка x_p(t)  и  h_r(t) 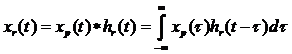        .                                                       (1)

Здесь  - импульсная характеристика (ИХ)  восстанавливающего фильтра,   - дискретный сигнал.

 

          Подставим в выражение свертки (1), получим

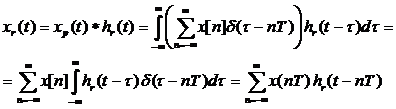
Найдем   h_r(t) – импульсную характеристику  восстанавливающего фильтра, как обратное преобразование Фурье от импульсной характеристики

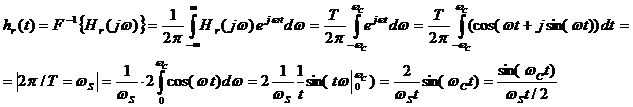
Примем, что частота среза идеального ФНЧ равна половине частоты отсчетов

.     Подставим эти значения  в  выражение импульсной характеристики 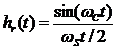   .      Получим .

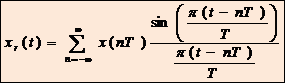 В результате  выражение  для  будет иметь вид                                                   .                                    (2)

 

Ряд (2)  называют интерполяционным рядом  Котельникова или рядом Шеннона.  Его члены имеют вид    с коэффициентами x(nT),  равными отсчетам сигнала  x(nT).  Графическая иллюстрация ряда

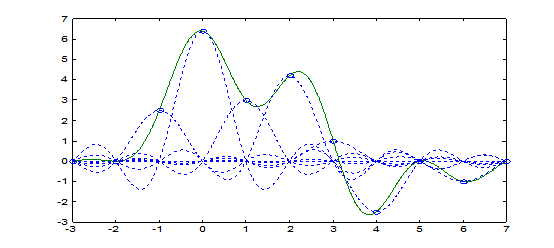
Этот ряд точно представляет исходный сигнал  x_a(t)  в точках отсчетов                     (n = )  и сходится к нему, т.е. интерполирует сигнал для всех промежуточных между отсчетами значений временной оси t.   Ряд (2) сходится очень медленно. Точное восстановление сигнала с помощью интерполяционного ряда Котельникова  требует:

 а) идеального ФНЧ,

 б) бесконечного числа членов самого ряда.     

 И то  и другое на практике невозможно обеспечить, поэтому для восстановления сигналов   применяются и  другие, более простые способы.

 

 

 

Восстановление  аналогового сигнала  с помощью
интерполяционного   полинома  нулевого порядка

 

На практике для восстановления непрерывного сигнала по его отсчетам широко используют восстановление с помощью полиномов нулевого порядка и полиномов первого порядка.

Для получения соответствующих интерполяционных выражений разложим сигнал  x(t) в точке отсчета t = nT в степенной ряд Тейлора

Чем выше порядок производной, тем большее число соседних отсчетов необходимо для её оценки. Это увеличивает точность восстановления, но усложняет интерполяцию сигнала. Поэтому на практике для восстановления сигналов по отсчетам чаще используют только первый член выражения разложения в ряд Тейлора и реже второй.  Для такой интерполяции необходима достаточно высокая частота отсчетов  по сравнению с граничным условием теоремы отсчетов  .

Использование только значений  x(nT) для  цифро – аналогового преобразования является наиболее простой аппроксимацией сигнала и называется интерполяцией полиномом нулевого порядка.   Соответствующие устройства называют эктраполяторами или фиксаторами  нулевого порядка (англ. Zero – Order Hold).  Такое устройство сохраняет значение непрерывного сигнала постоянным до поступления следующего отсчета, т.е.  экстраполирует сигнал:

Рассмотрим процесс восстановления более подробно с  использованием импульсной и частотной характеристик такого интерполятора.

 

 

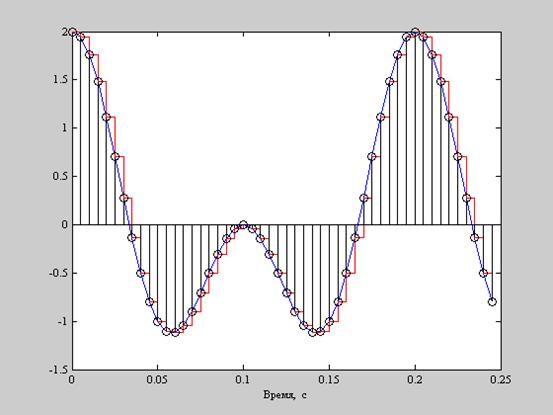
Импульсная характеристика, т.е. реакция на δ – функцию, фиксатора нулевого порядка  h₀(t)  имеет вид (Т – интервал отсчетов). Восстановленный сигнал – свертка h₀(t)  и x (nT).

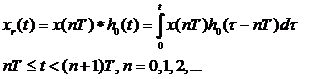
  Частотная характеристика интерполятора нулевого порядка  как преобразование Фурье импульсной характеристики

График АЧХ  и ФЧХ такого фиксатора  при Т = 1 в зависимости от частоты  f

 

 

Частотная характеристика фиксатора изменяется по закону sin(x)/x , т.е. имеет пульсирующий характер. По сравнению с частотной характеристикой  идеального ФНЧ  фиксатор нулевого порядка имеет высокочастотные составляющие пульсирующего характера. При уменьшении периода отсчета Т АЧХ фиксатора становится ближе к АЧХ идеального ФНЧ, но высокочастотные пульсации АЧХ все равно остаются, и для уменьшения пульсаций выходного сигнала ЦАП необходим сглаживающий ФНЧ.

 Фазовая характеристика  интерполятора – линейная, поэтому фазовых искажений  такой интерполятор не вносит

 

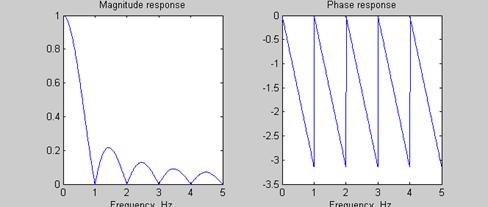
Неизменные спутники такой интерполяции – «ступеньки» -  сглаживаются  с помощью выходного ФНЧ.

Примечание. В основном (базовом)  MATLAB имеется функция интерполяции временной последовательности ST = SETINTERPMETHOD(TS,METHOD), в которой TS – последовательность отсчетов,  METHOD – строка, устанавливающая метод интерполяции. Она может иметь 2 значения:    'zoh' (zero-order hold) – для установки интерполяции полиномом первого порядка и 'linear' – интерполяция полиномом первого порядка.  Ознакомьтесь и протестируйте эту функцию на сигнале s .

 

 

Восстановление  аналогового сигнала  с помощью
интерполяционного   полинома первого  порядка

 

Кроме  полинома нулевого порядка для восстановления аналогового сигнала по его отсчетам часто используются также полиномы первого порядка, в которых кроме отсчета сигнала  необходима также его первая производная в момент отсчета. Устройство восстановления на основе полинома первого порядка называется экстраполятором (фиксатором) первого порядка (англ. First – Order Hold).

Выражение восстановленного сигнала

                                        .

Используются только первые 2 члена ряда Тейлора.

При этом первая производная в момент t = nT может быть приближенно вычислена по формуле               (интерполирование вперед),

или по формуле      (интерполирование назад).

Таким образом, такое восстановление – более сложное по сравнению с использованием полинома нулевого порядка, т.к. необходимо на каждом шаге вычислять оценку  производной сигнала.

В графическом представлении при этом способе восстановления  соседние отсчеты соединяются прямыми линиями. Такой способ обычно используется в компьютерных программах при построении графиков функций, он называется линейной интерполяцией.

           

 

 

 

 

Импульсная характеристика экстраполятора первого порядка (Т – интервал отсчетов)

 

 

 

 

 

 

 

 

 

Найдем   частотную характеристику  интерполятора первого порядка

Частотная характеристика  интерполятора первого порядка как преобразование Фурье импульсной характеристики

 

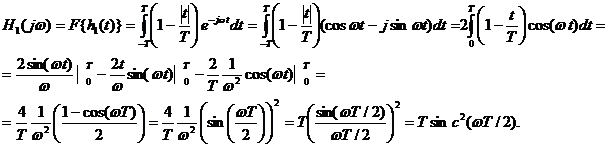
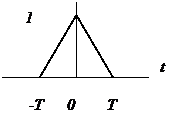 Графики АЧХ  интерполяторов  нулевого  и первого порядка при Т = 1

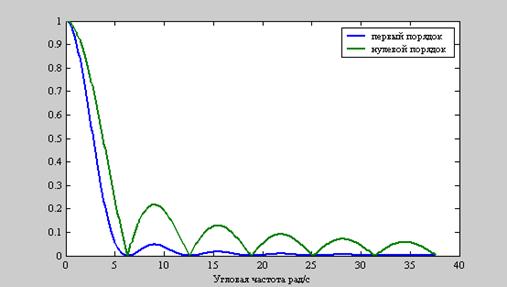
Как следует из графиков, АЧХ  фиксатора первого порядка имеет более крутой спад основного низкочастотного лепестка и главное -  существенно более низкий уровень пульсаций высокочастотных составляющих. Высокочастотные составляющие шума, сопровождающего процессы АЦП и ЦАП, подавляются идеальным ФНЧ.Но такой фильтр практически не реализуем.  Интерполятор первого порядка подавляет эти составляющие в значительно большей степени, чем интерполятор нулевого порядка . Поэтому он обеспечивает меньший уровень пульсаций, чем фиксатор нулевого порядка. Однако такой способ – более сложный, так как в каждой точке необходимо вычисление первой производной сигнала.

Примечание.  Рассмотрение приближения (аппроксимации) функций  полиномами нулевого и/или  первого порядка во временной области – это обычный метод вычислительной математики, в частотной области – это метод, принятый в обработке сигналов.

В каждой области науки предпочитают использовать  свои методы и инструменты.

Заключение

 

§  Для восстановления аналогового сигнала по его отсчетам используется цифро – аналоговое  преобразование (ЦАП) сигнала.

§  Из теоремы отсчетов и модели цифро – аналогового преобразования сигнала в частотной области  следует, что спектр исходного аналогового сигнала может быть точно восстановлен фильтрацией идеальным фильтром нижних частот, если при дискретизации соблюдаются требования теоремы отсчетов.

§  Во временной области аналоговый сигнал может быть точно восстановлен из отсчетов с помощью интерполяционного полинома Котельникова,
                                  .

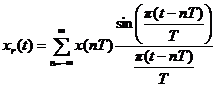Ряд сходится медленно. Точное восстановление сигнала с помощью интерполяционного ряда Котельникова требует:

 а) идеального ФНЧ,

 б) бесконечного числа членов самого ряда.

    И то  и другое на практике невозможно обеспечить, поэтому практически возможно только приближенное восстановление сигнала по отсчетам. Тем не менее интерполяционный полином Котельникова очень важен как теоретический результат.

§  На практике для приближенного восстановления аналогового сигнала по его отсчетам широко используются  полиномы (интерполяторы)  нулевого и первого порядка при частоте отсчетов,  необходимой для требуемой  точности восстановления.