Понятие  сигнала и системы

В широком смысле сигналы – носители информации в информационных системах.   Термин  охватывает   аудио, видео, речевые, музыкальные, медицинские, геофизические  и другие самые разнообразные виды сигналов. Последовательность команд компьютера – это тоже сигнал, поскольку она несет  определенную информацию.

 В более узком смысле, характерном для курса ТОС или подобного ему, сигнал  (signal) – физическая величина, которая изменяется в зависимости от времени или пространственной переменной или вектора (набора) независимых переменных.

  Примеры сигналов:

a) Одномерный сигнал –напряжение на выходе термопары (termocouple signal)  в зависимости от времени – u(t).

б)  Речевой сигнал (speech signal) – сумма гармоник с изменяющимися во времени амплитудами, частотами и фазами. Частоты гармоник 20 Гц – 20 кГц

^. 

   Пример фрагмента речевого сигнала

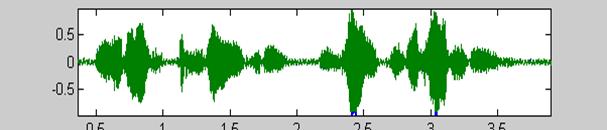
На данном рис. горизонтальная ось – ось времени в секундах, вертикальная ось уровень речевого сигнала. В одной секунде – 44100 отсчетов сигнала.

 

в)  Сигнал  изображения (image signal) –двумерный сигнал  I(x,y).   Яркость (интенсивность)  изображения  I(x,y)– функция I двух пространственных координат точки  (x,y).

           

г) Сигнал цветного телевидения (color TV – signal) -  трехмерный  сигнал, формируемый из трех отдельных монохромных составляющих – красной (r), зеленой (g) и синей (b).

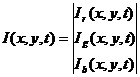
Система – физическое устройство,  выполняющее определенные операции над сигналами. В курсе ТОС рассматриваются  математические модели преобразования сигналов. Нотация:    или  , L – оператор преобразования входного сигнала.  Если операции над сигналами – линейные  (оператор  L – линейный), то система является  линейной. Для линейных систем справедлив принцип суперпозиции: если , то  ,  т.е. линейной комбинации входных сигналов соответствует такая же линейная комбинация выходных сигналов.

Классификация  сигналов

1.        Детерминированные и случайные сигналы

Детерминированный сигнал представляется как функция аргумента (аргументов) и может быть определен для любого значения аргумента из области определения функции. Например, гармонический сигнал    - функция косинуса от времени.

 Случайными являются сигналы, значения которых заранее неизвестны и могут быть описаны только статистически, т.е. вероятностными моделями и характеристиками.
Новую информацию могут нести только случайные сигналы. Детерминированные сигналы широко используются как тестовые при анализе систем.

2.   Непрерывные (continuous time) и дискретные (discrete time) по времени сигналы
Непрерывные по времени (НВ) или аналоговые сигналы задаются на несчетном множестве точек аргумента и могут принимать действительные или комплексные значения.  Такие сигналы в данном курсе будут обозначаться как x(t), y(t) и т.д. Дискретные по времени (ДВ) или дискретные сигналы определяются на счетном множестве значений аргумента и обозначаются как x(nT_S) = x[n], где T_S – интервал отсчетов.  Т.е.,  при обозначениях непрерывных сигналов будут использоваться круглые скобки, а дискретных – квадратные скобки. Модель отсчетов:  замыкание – размыкание  ключа  с периодом Т_S.

Сигналы  могут быть также непрерывными или дискретными не только по аргументу, но и по значению (уровню).   Непрерывные по аргументам  и значениям сигналы называют также аналоговыми, дискретные по времени и значению сигналы -  цифровыми. В настоящее время цифровые сигналы и их  обработка (ЦОС) занимают ведущее положение в большинстве практических задач.   Для преобразования  аналоговых сигналов в цифровые используются аналого-цифровые преобразователи (АЦП), для обратного преобразования – цифроаналоговые преобразователи (ЦАП).

3.        Действительные и комплексные сигналы

Сигналы реального мира (real world signals) являются действительными.  Тем не менее в задачах обработки сигналов очень часто рассматриваются  комплексные сигналы.

Их  использование упрощает анализ сигналов  и расчетные соотношения.

Например,  гармоническому сигналу    

можно поставить в соответствие  комплексную гармонику с периодом    

 -  компл. амплитуда.

При этом  действительная гармоника   .

Аналогично 

Графики  и   для 

Компоненты  и   называют квадратурными составляющими сигнала.

Преимущества использования комплексного исчисления заключается в возможности замены операций дифференцирования и интегрирования простой операцией умножения. Действительно, пусть дан комплексный сигнал в виде комплексной гармоники .  Тогда производная этого сигнала 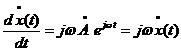, т.е. дифференцирование сводится к умножению комплексной величины на jω.  Аналогично при операции интегрирования   выполняется умножение сигнала на –j/ω.  

Физический смысл приписывается действительной части  комплексного результата.

Энергия,  мощность и автокорреляционная функция сигнала

Мощность, рассеиваемая в резисторе R при напряжении U,  равна  .

Если к резистору приложено переменное напряжение (сигнал) x(t), то мгновенная мощность, рассеиваемая в резисторе будет

.

Энергия E, выделяемая  в резисторе за время T  - интеграл от мощности

.

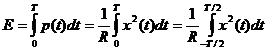Средняя мощность за время T

.

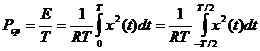В теории сигналов принято рассматривать энергию и мощность при сопротивлении            R =1 Ом.     Тогда  энергия и средняя мощность непрерывного  по времени (НВ) сигнала

,       .

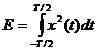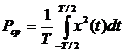Для сигнала  x(t), определенного на всей временной оси  

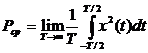
Квадратный корень из средней мощности называется среднеквадратичным значением сигнала             .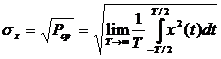

Выражения энергии и мощности для дискретного во времени (ДВ) сигнала x[n]

,

              при        ,     .

Сигналы  являются  сигналами с конечной энергией, если энергия   и с конечной мощностью, когда мощность .

Автокорреляционная функция (АКФ) детерминированного сигнала x(t) – это интеграл вида     , т.е. интеграл от двух копий сигнала, сдвинутых относительно друг друга на интервал τ. АКФ часто используется на практике.  Свойства АКФ

1.        Значение АКФ при    равно энергии сигнала,   .

2.        АКФ является четной функцией аргумента τ, т.е.  .

3.        Для сигнала с конечной энергией при увеличении аргумента АКФ затухает
                               .

4.        Значение АКФ при τ = 0 является наибольшим значением  .

 

 

В качестве примера найдем АКФ прямоугольного импульса

 

 

При  сдвиге                      ,

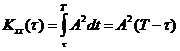Для                                               .

Отсюда, объединяя результаты, получаем

                                                

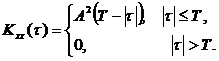
График АКФ прямоугольного импульса

При увеличении  сдвига  τ

АКФ вначале линейно  возрастает,

затем линейно убывает.

Для сигналов ДВ  x[n] автокорреляционная функция  определяется выражением

    .

Как частный случай при нулевом сдвиге l = 0 имеем

                                                 -  энергия сигнала ДВ.

Максимальная автокорреляция достигается при  l = 0, т.е. при нулевом сдвиге.

Для дискретных сигналов также   , т.е. автокорреляционная последовательность является четной функцией аргумента.

Понятие  корреляции может быть обобщено на случай  зависимости двух сигналов.

При этом получаем взаимную корреляционную функцию (ВКФ), которая является мерой сходства  сигналов  x(t) и y(t).

                Для сигналов НВ (аналоговых сигналов) ВКФ

                                               ,

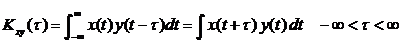для сигналов ДВ

                                              

                В MATLAB для вычисления взаимной корреляции и автокорреляции служит функция   k =xcorr(x,y). При этом xcorr(x)  вычисляет автокорреляционную последовательность сигнала x[n].

Биомедицинские сигналы

                Биомедицина – одна из популярных областей приложений обработки сигналов, особенно в последние десятилетия.

 Большинство физиологических процессов в живом  организме сопровождается появлением сигналов.  Болезни или дефекты в организме  приводят к патологическим процессам, т.е. к изменениям в нормальных физиологических процессах.  В результате  при наличии той или иной патологии сигналы могут отличаться от нормальных сигналов и использоваться для диагностики заболеваний.

Основные биомедицинские сигналы:

·       Электрокардиограмма (ЭКГ) – электрический сигнал, появляющийся в результате электрической активности сердца и регистрируемый с помощью поверхностных электродов, размещаемых на груди и конечностях.

·       Электроэнцефалограмма (ЭЭГ) – сигналы электрической активности мозга, которые могут быть записаны с поверхности кожи головы с использованием поверхностных электродов. Сигнал ЭЭГ может использоваться для изучения состояния нервной системы, наблюдения стадий сна, для диагностики ряда заболеваний и др. целей.

·       Электронеймограмма (ЭНГ) – электрический сигнал, появляющийся, когда стимул и связанный с ним электрический потенциал действия  распространяется вдоль нерва и регистрируется с помощью специального игольчатого электрода.

·       Фонокардиограмма (ФКГ) – звуковые  сигналы,  возникающие в связи с сокращениями сердца и кровеносных сосудов. Акустические сигналы звуков сердца прослушиваются с помощью стетоскопа или преобразуются в электрические сигналы с помощью размещаемых на теле пациента микрофонов и датчиков давления.

·       Электрогастрограмма (ЭГГ) – сигнал электрической активности желудка, регистрируемый с помощью наружных электродов, размещаемых на  животе пациента,

·       Речевые сигналы (РС) -  обычные сигналы речи,  используемые как диагностические при нарушениях звукового и речевого трактов пациента.

·       Электромиограмма (ЭМГ) – сигнал электрической активности сокращающихся  волокон мышц, регистрируемый с помощью специальных игольчатых электродов. Некоторые заболевания влияют на форму сигнала ЭМГ.

Характерные особенности биомедицинских сигналов:

§  Низкий уровень потенциала (10 мкВ – 10 мВ),

§  Низкочастотный диапазон (от постоянного тока, т.е. 0 Гц до нескольких сотен Гц).

§  Сильное влияние артефактов  - помех от электродов, движения головы, мышц тела, помех от линий электропитания, окружающего  электро -  и радиооборудования, электромагнитных  полей и др. Артефакты снижают информативность сигналов и усложняют их анализ, поскольку полезный сигнал – низкоуровневый.  Необходима  специальная обработка этих сигналов  для получения неискаженных данных.

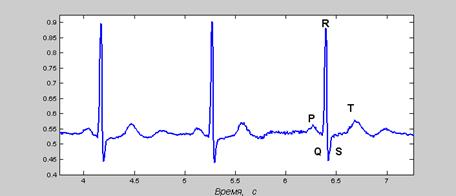
 На рис. представлен вид  сигнала ЭКГ.  Характерными фрагментами сигнала  являются  P - зубец, возникающий при медленном сокращении предсердий,  QRS – комплекс длительностью около 80 мс из-за сокращения желудочков сердца, и  ST – сегмент, соответствующий фазе расслабления  (реполяризации) желудочков.

Размах сигнала ЭКГ в норме равен примерно  1 мВ, полоса частот клинической ЭКГ 0,05 – 100 Гц.

 

Заключение

§ Основной задачей курса является изучение математических моделей сигналов и их обработки в линейных системах. Линейные системы очень широко используются на практике, в частности, в аудиосистемах,  видеосистемах, измерительных системах,  медико - технических приложениях.

§ В качестве инструментальной среды расчетов, анализа  и моделирования в  лабораторном практикуме по курсу  используется система MATLAB фирмы  MathWorks,  Inc.

§ Сигнал – физическая величина, изменяющаяся в зависимости от времени или/и пространственной переменной или набора (вектора) переменных (многомерные сигналы).

§ Сигналы подразделяются на:
- детерминированные и случайные,
- непрерывные по времени (НВ) и дискретные по времени (ДВ) сигналы,
- действительные  и комплексные.
Возможны также другие  признаки классификации.

§ Важными измерениями (характеристиками) сигнала являются его энергия 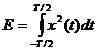        и средняя мощность   .

Автокорреляционная функция (характеристика) сигнала     выражает меру сходства (подобия) сигнала  и его копии, сдвинутых друг относительно друга на значение τ.       При .