Быстрое преобразование Фурье .
Общие сведения.
Пара ДПФ, т.е. прямое и обратное ДПФ, определяются выражениями
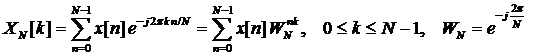 ,
,
![]()
Здесь N – размер (длина) ДПФ.
В общем случае x[n] -
комплексный сигнал. Поэтому
прямое вычисление X[k] для ![]() требует N2 комплексных
умножений и
требует N2 комплексных
умножений и ![]() комплексных сложений (сложение N слагаемых требует N-1 операций).
Комплексное умножение двух чисел состоит из 4-х умножений и трех сложений
действительных чисел. С увеличением N число операций ДПФ возрастает квадратично. Для больших
N порядка 500 и больше вычисление ДПФ требует достаточно
большого времени. Например, если одно
комплексное умножение занимает 50 мксек, то для N=1000 время вычисления составляет не менее 50 сек.
Для компьютеров 60 – 70-х г.г. с их низким быстродействием время
вычисления ДПФ могло составлять несколько часов. ДПФ широко используется,
поэтому остро стоял вопрос о повышении его скорости вычислений.
комплексных сложений (сложение N слагаемых требует N-1 операций).
Комплексное умножение двух чисел состоит из 4-х умножений и трех сложений
действительных чисел. С увеличением N число операций ДПФ возрастает квадратично. Для больших
N порядка 500 и больше вычисление ДПФ требует достаточно
большого времени. Например, если одно
комплексное умножение занимает 50 мксек, то для N=1000 время вычисления составляет не менее 50 сек.
Для компьютеров 60 – 70-х г.г. с их низким быстродействием время
вычисления ДПФ могло составлять несколько часов. ДПФ широко используется,
поэтому остро стоял вопрос о повышении его скорости вычислений.
В
Для N=2 m этот алгоритм требует приблизительно ![]() комплексных
умножений и сложений, т.е. алгоритм быстрее в
комплексных
умножений и сложений, т.е. алгоритм быстрее в ![]() раз.
раз.
Для N=1024 алгоритм БПФ быстрее примерно в 1024/10=102,4 раз, для N = 4096 – в 340 раз и т.д. Чем больше N, тем больше выигрыш во времени. С использованием БПФ стало возможным вычисление ДПФ в реальном времени (on - line).
В настоящее время под БПФ понимается достаточно большой набор алгоритмов, в том числе алгоритм с прореживанием по времени, алгоритм с прореживанием по частоте, алгоритм Герцеля, алгоритм Винограда и др. Имеется много отработанных программ вычисления БПФ на различных языках программирования (см., например, программу БПФ на языке С++ в статье «Быстрое преобразование Фурье» Википедии).
В опубликованных источниках и сайтах Internet можно найти множество вариантов программ БПФ.
Если ![]() , тогда общее число операций БПФ есть
, тогда общее число операций БПФ есть ![]() . При вычислении БПФ последовательность x1,, x2, …, xN длиной N точек разбивается на m подпоследовтельностей длиной r1, r2,… ,rm. Для каждой из них определяется ДПФ и затем на основе
соответствующего алгоритма БПФ вычислется пребразование Фурье всей последовательности. При этом число Коп значительно
меньше N2
– числа операций, требуемого для прямого вычисления ДПФ.
Если все множители N одинаковы,
т.е.
. При вычислении БПФ последовательность x1,, x2, …, xN длиной N точек разбивается на m подпоследовтельностей длиной r1, r2,… ,rm. Для каждой из них определяется ДПФ и затем на основе
соответствующего алгоритма БПФ вычислется пребразование Фурье всей последовательности. При этом число Коп значительно
меньше N2
– числа операций, требуемого для прямого вычисления ДПФ.
Если все множители N одинаковы,
т.е. ![]() , так что
, так что ![]() , то
, то ![]() . В таком случае
говорят, что алгоритм БПФ имеет основание,
или базу
r. Наиболее часто используются алгоритмы с
основаниями 2 и 4. При основании 2 количество операций
. В таком случае
говорят, что алгоритм БПФ имеет основание,
или базу
r. Наиболее часто используются алгоритмы с
основаниями 2 и 4. При основании 2 количество операций ![]() . Дополнительно можно
уменьшить количество умножений – сложений
до
. Дополнительно можно
уменьшить количество умножений – сложений
до ![]() за счет использования
периодичности ДПФ.
за счет использования
периодичности ДПФ.
Вслед за БПФ появились и используются алгоритмы быстрого преобразования Уолша, Хартли, вейвлетного преобразования и др., используемые в обработке сигналов.
Алгоритм БПФ с прореживанием по времени
Исторически первым и широко используемым до
настоящего времени является алгоритм
прореживания во времени, предложенный американскими учеными
Cooley and Tukey (
Основная идея алгоритма БПФ с прореживанием по времени состоит в том, чтобы разбить исходную N-точечную последовательность на две более короткие последовательности, ДПФ которых образуют ДПФ N-точечной последовательности. Для вычисления ДПФ двух (N/2) – точечных последовательностей потребуется (N/2)2·2 = N2/2 умножений, т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения на две последовательности можно повторить (рекурсия), сокращая тем самым объем вычислений ещё в 2 раза и т.д., пока не получится 2-х точечное БПФ. После этого вычисляются БПФ двухточечных последовательностей и они используются для вычисления ДПФ всей последовательности. Рассмотрим алгоритм подробнее.
Исходное выражение ДПФ:
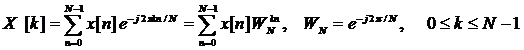 (1)
(1)
Последовательность ![]() длиной N отсчетов разделим на две
последовательности с четными и нечетными
отсчетами по N/2 отсчетов
каждая
длиной N отсчетов разделим на две
последовательности с четными и нечетными
отсчетами по N/2 отсчетов
каждая
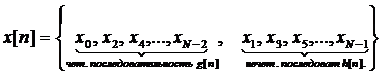 . Тогда
. Тогда
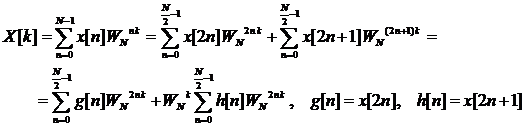 . (2)
. (2)
Суммы в выражении (2) представляют собой ДПФ размерности N/2.
Поскольку ![]() , то
, то 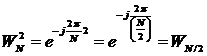 , т.е.
, т.е. ![]() .
.
Поэтому выражение (2) для X[k] можно записать в виде
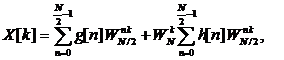 . (3)
. (3)
Первая сумма - это ДПФ четной последовательности g[n], вторая – нечетной h[n].
Тогда, если обозначить
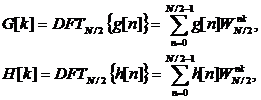 - ДПФ
размером N/2,
(4)
- ДПФ
размером N/2,
(4)
то
![]() .
(5)
.
(5)
ДПФ
размерности N/2 имеет период N/2 и выражение (5) можно использовать только
для ![]() .
.
Для остальных ![]() можно воспользоваться
свойством периодичности ДПФ
можно воспользоваться
свойством периодичности ДПФ
![]() . (6)
. (6)
Учитывая, что ![]() ,
,
выражение
для N – точечного ДПФ можно записать как сумму двух ДПФ размерности N/2.
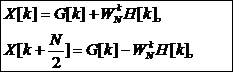 (7)
(7)
Уравнения (7) можно
изобразить графически. Получится наглядный граф вычислений, названный «бабочкой» БПФ
Согласно уравнениям (7) результатом вычислений будут X[k] и X[k+N/2].
Входные данные для
«бабочки» слева, выходные – справа. При
вычислении верхнего выражения применяется суммирование с весовым коэффициентом ![]() , при вычислении нижнего – вычитание с тем же весом. Т.е., в верхнем направлении по «бабочке»
положительный весовой коэффициент, в нижнем – отрицательный. Значения комплексной
экспоненты
, при вычислении нижнего – вычитание с тем же весом. Т.е., в верхнем направлении по «бабочке»
положительный весовой коэффициент, в нижнем – отрицательный. Значения комплексной
экспоненты ![]() в данном контексте называют
множителями вращения (twiddle factors).
в данном контексте называют
множителями вращения (twiddle factors).
Выражения (7) вычисляют то же ДПФ, что и выражения (1) или (2), но являются ДПФ размером N/2, поэтому вычисляются в 2 раза быстрее.
Диаграмма (граф) вычислений по выражению (7) для N = 8
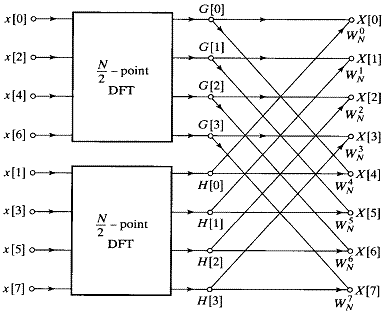
Начало вычислений – слева. Данные x[n] разделяются
на четную и нечетную (по индексам) части.
Для каждого подмножества имеем ДПФ размером
N/2 = 4. Значения G[k]
– 4- х точечное ДПФ для четных индексов x[n], H[k] – для нечетных. В соответствии с формулой (7) или
схемой графа G[k] и H[k] используются для вычисления значений X[k]. Например,
![]() .
.
На этом возможности по ускорению вычисления ДПФ не заканчиваются.
Вторая основная концепция БПФ - алгоритма – это рекурсия, т.е. повторение разбиения. Предположим, что N/2 –тоже четное число. Тогда каждая из последовательностей g[n] и h[n] разбивается на две последовательности, состоящие тоже из четных и нечетных номеров членов.
Каждая из этих последовательностей имеет теперь длину N/4:
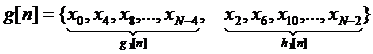 ,
,
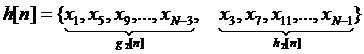
Для каждой из
последовательностей ![]() вычисляется ДПФ размером N/4.
вычисляется ДПФ размером N/4.
При этом N/2 – точечные ДПФ будут вычисляться как комбинации ДПФ размером N/4. Здесь снова обеспечивается увеличение скорости вычислений в 2 раза.
Если N = 2m, то процесс деления пополам выполняется m раз, пока не получится последовательность gm[n], которая содержит всего две точки.
Из общего выражения ДПФ 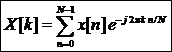
При N=2, т.е. для n, k = 0,1 получаем выражения двухточечного БПФ
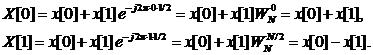 (8)
(8)
Граф («бабочка») 2-х точечного ДПФ
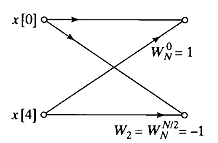
Следовательно, для вычисления двухточечного БПФ требуются только операции сложения и вычитания без операции умножения.
В результате для N- точечного ДПФ число
требуемых операций умножения - сложения уменьшается до ≈ ![]() . Точнее, для БПФ требуется
. Точнее, для БПФ требуется ![]() операций комплексного умножения по сравнению c N2 при обычном БПФ и
операций комплексного умножения по сравнению c N2 при обычном БПФ и ![]() операций комплексного сложения в сравнении с N(N-1)
операциями обычного ДПФ.
операций комплексного сложения в сравнении с N(N-1)
операциями обычного ДПФ.
Схема (граф) вычисления 8
-точечного БПФ
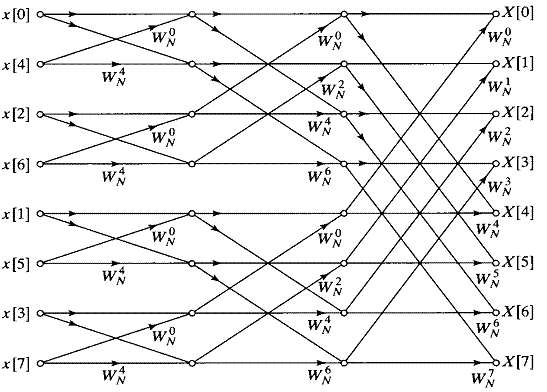
8-точечное БПФ с
основанием 2 вычисляется как окончательный результат с использованием трех
каскадов. Восемь входных
отсчетов из временной области сначала разделяются (или прореживаются)
на четыре группы для
вычисления 2-точечных ДПФ. Затем четыре 2-точечных ДПФ объединяются в два 4-точечных ДПФ. На заключительном этапе два 4-точечных ДПФ объединяются для того,
чтобы получить окончательный
результат X(k) - 8-точечное ДПФ.
Алгоритм БПФ с прореживанием по времени требует такой
перестановки входной последовательности x[n], чтобы выходная последовательность ![]() имела естественный
порядок расположения результатов
имела естественный
порядок расположения результатов ![]() . Если N является
степенью 2, то входная последовательность x[n]
перед вычислением ДПФ должна располагаться в памяти в так называемом двоично-инверсном (реверсивном) порядке.
. Если N является
степенью 2, то входная последовательность x[n]
перед вычислением ДПФ должна располагаться в памяти в так называемом двоично-инверсном (реверсивном) порядке.
Характер двоичного реверсирования: исходный двоичный номер (индекс элемента массива) 10010 à двоично - реверсивный номер 01001. Отсчеты исходной последовательности сигнала располагаются в порядке следования двоично-инверсных номеров членов последовательности. При этом биты, симметрично расположенные относительно центра, меняются местами.
Пусть, например, исходная 8-ми точечная последовательность имеет вид
x[n] = {2, 1, 0, 8, 2, 4, 3, 5}. В памяти перед выполнением БПФ элементы вектора сигнала должны быть переставлены следующим образом.
Исходный порядок à Порядок после перестановки
Десятичный Двоичный x[n] Двоично Десятичный x
номер индекс реверсивный номер
0 000 2 000 0 2
1
001 1 100 4 2
2 010 0 010 2 0
3 011 8 110 6 3
4 100 2 001 1 1
5 101 4 101 5 4
6 110 3 011 3 8
7 111 5 111 7 5
Имеются специальные алгоритмы для быстрой двоично-реверсивной перестановки данных. Они и используются на начальном этапе вычисления БПФ.
Алгоритм
БПФ с прореживанием по частоте. Особенности:
· Основой операцией является «бабочка БПФ», в которой
выполняется умножение на ![]() ,
,
· Входная последовательность xn n=0,1,…,N-1, N=2m имеет естественный
порядок следования номеров отсчетов,
· На каждой ступени вычисления БПФ входная
последовательность разбивается на две,
· Выходная последовательность переставляется по правилу
двоичной арифметики.
·
Краткое
заключение по рядам и преобразованиям Фурье
· В лекциях 4-8 курса рассматривались ряды и преобразования Фурье, являющиеся теоретической основой спектрального (частотного) анализа сигналов и частотных методов анализа и синтеза линейных систем. Ниже в таблице представлены краткие итоги изложенного материала.
|
Вид преобразования |
Сигнал во временной области |
Сигнал в частотной области |
Свойство свертки |
|
Преобразование Фурье НВПФ (CTFT)
|
непрерывный |
непрерывный |
|
|
Ряд Фурье НВРФ (CTFS)
|
непрерывный периодический (T) |
дискретный |
|
|
Дискретное преобразование Фурье ДПФ (DFT)
|
дискретный периодический (N) |
дискретный периодический (N) |
|
·
Заключение
§
Быстрое
преобразование Фурье (БПФ, FFT) – это
алгоритмы для ускоренного вычисления ДПФ путем сокращения требуемого
числа операций умножения и сложения. Данные алгоритмы получили исключительно
широкое применение в приложениях обработки сигналов, сжатия данных, ядерной физики, вычислительной
математики и в других областях.
Для цифровой обработки сигналов появление БПФ означало революционное достижение.
§ Одним из наиболее популярных алгоритмов
БПФ является алгоритм с прореживанием по
времени. Идея
алгоритма БПФ с прореживанием по
времени заключается в разбиении исходной N-точечной последовательности на две более короткие
последовательности, ДПФ которых образуют
ДПФ N-точечной последовательности. Для вычисления двух (N/2) – точечных последовательностей потребуется (N/2)2·2 = N2/2 умножений, т.е. вдвое меньше по сравнению с прямым
вычислением. Операцию разбиения на
две последовательности повторяется
(рекурсия), сокращая тем самым объем вычислений ещё в 2 раза и т.д. На заключительном этапе разбиения вычисляются простейшие 2-х точечные ДПФ, и
они используются путем соответствующих вычислений для получения ДПФ
размерности N.
§ Если размер
ДПФ ![]() , то общее число
операций БПФ равно
, то общее число
операций БПФ равно ![]() . Это число меньше N2 – числа операций, требуемого для прямого
вычисления ДПФ. Наибольший
выигрыш по количеству операций умножения – сложения достигается при размере
ДПФ N = 2m. В этом случае количество операций
. Это число меньше N2 – числа операций, требуемого для прямого
вычисления ДПФ. Наибольший
выигрыш по количеству операций умножения – сложения достигается при размере
ДПФ N = 2m. В этом случае количество операций ![]() по сравнению с N2 для
прямого вычисления ДПФ.
по сравнению с N2 для
прямого вычисления ДПФ.
§ Другими распространенными алгоритмами БПФ являются
алгоритм с прореживанием по частоте, алгоритм
Герцеля,
алгоритм Винограда и др.